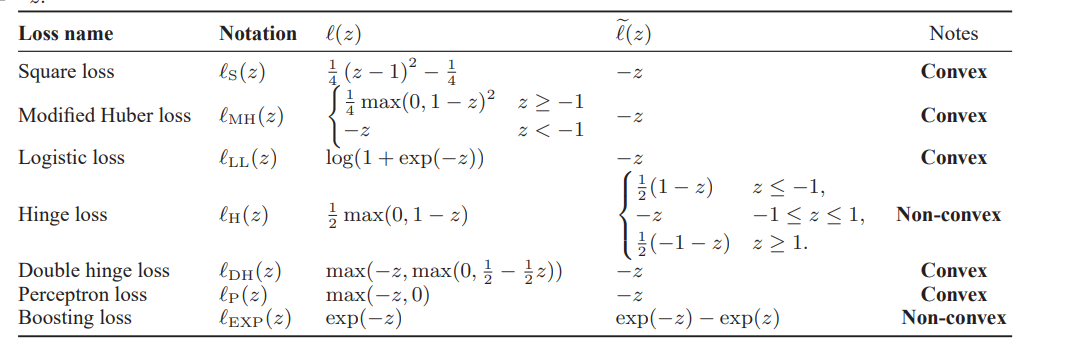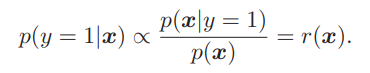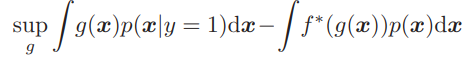Sen(Qian)’s Memo

https://proceedings.mlr.press/v37/plessis15.html

のちの手法のベンチマークの基準となるuPUである。

PUの現実への応用として以下のようなものがある。

• 画像の分類　ユーザが一部の写真を選び出して、それをもとに写真全体でのカテゴリ分けを行う。
• 異常値検出　正常値のみを含むデータセットを与えられて学習する。そして、与えられたUnlabeledのデータセットの中から異常値を見つける。
• Negative例があまりにも多すぎる場合　異常値検出と似ているがone vs restのようにPUを使うこともできる。
• Negativeサンプルの分布シフト　訓練データとテストデータのNegative例の分布が違ってくる。普通はテストデータに対応するようなNegativeサンプルを生成しないといけない。しかし、PUでUをNegative例を含むようにすれば、普通のPUで解決できる。
  • スパムメールがNegativeとする。普通のメール=Pの特徴は不変だが、スパム=Nは常に変わりうる。
  • この時にNegative例の変更に対して追加で訓練しなくてもそれなりの性能がある。

同じ研究グループの先行研究 📄2014-NIPS-[Ramp]Analysis of Learning from Positive and Unlabeled Data では、Ramp損失により$l(z) + l(-z) = 1$によって定数項を作りだし、最適化をしやすくした。だが、Ramp損失は非凸なので最適化が難しいというのが織り込み済みではあったが、ここを何とか改善したのがこの論文。

先行研究 📄2014-NIPS-[Ramp]Analysis of Learning from Positive and Unlabeled Data では$l(z) + l(-z) = 1$を作り出していたが、この論文では式変形で、$l(z) - l(-z)$を作り出したい。

もともとは以下の損失の式から導いていた。

このように、Unlabeldのデータの期待値から展開して得ることができ、これによって得られない$\mathbb{E}_{-1}$の期待値を代わりに計算ができる。ただ代入すると今回の論文で提案した式になるが、先行研究では$\mathbb{E}_1[l(g(X))] = 1 - \mathbb{E}_{1}[l(-g(X))]$とすることでうまく$l(z) + l(-z)$の形を作り出した。ここでの意味としては、Positiveデータにおいて、Positiveだと判定される確率とNegativeだと判定される確率の和は1であるからを利用している。そのように代入した結果が以下の式になる。

今回は、上の式を導いたオリジナルの式$R(f) = \pi R_1(f) + (1 - \pi) R_{-1}(f)$から再度式変形をする。$\mathbb{E}_X[l(-g(X))]$を用いて代入すると以下のようになる。ここで、$R_X(f)$の展開から$\mathbb{E}_1[l(g(X))] = 1 - \mathbb{E}_{1}[l(-g(X))]$をしていないことに注目。

ここで、$l(z) - l(-z)$が凸関数になれば、全体で凸の最適化になれそうなのでうれしい気持ちになる。先行研究とはまた別の方向での改善提案。

$l(z)$が凸関数である場合、$l(z) - l(-z)$も凸関数というか線形関数である(証明略　凸関数の定義は一回微分を見ればいいのでそれを使って少しやればできる)。よって、本論文では簡単のため、ここで指す線形関数は$-z$、すなわち

であると考える。

後はこの論文ではカーネル法を使ったSVMを識別器として、Empiricalの場合がどうなっているかを説明している。

ここで、$\tilde{l}(z) = l(z) - l(-z)$である。

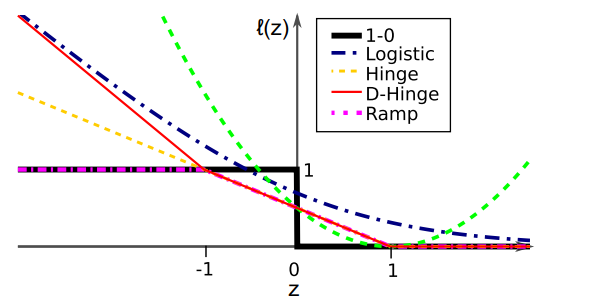
関数の概形は以下の通り。

この論文で提案されたのはDouble Hinge Lossである。

外れ値検出についての議論をする。PUで、Pを正常値として扱うことで外れ値検出のフレームワークができる。

ここで、密度比$r(x)$について、

1. $p(x|y=1). p(x)$をPUのデータセットから学習して推定する。
2. 割って計算する。

2ステップを踏むことになるが、2つも推定を挟むと、ただでさえ信用度が低い高次元データの密度推定を除算に使うと、値のブレが激しくなる($p(x)$とかぶれたらつらいよね)。ならば、直接推定しよう。先行研究では以下のように推定している。

(ここから下よくわからないので訳をただ載せているだけ)

ここでは、$f$は凸関数で$f(1)=0$を満たす。

ここで、$f(t)$ は凸関数で $f(1) = 0$ を満たし、$f^*(z) = \sup_t (tz - f(t))$ はそのフェンシェル双対を表します(双対はより最適化しやすい形に変換している)。上の式は、 $p(x|y = 1)$から $p(x)$ への f -divergence の下限です。(f-divergenceはKL-divergenceのlogを任意の関数$f$にしたもの)

f-divergenceについての考察

supを含む式は、 $g = r$ で最大化され、 $r(x) \in \partial f^*(g(x))$ （つまり、解は密度比の関数です）。この推定器は、Smola et al.（2009）におけるKullback-Leibler発散（Kullback & Leibler, 1951）下での正常値ベースの外れ値検出や、Hido et al.（2008）におけるPearson発散（Pearson, 1900）下で使用されています。

一方、PU分類では、クラス後確率の差の符号に関心があります：

これにも密度比 $r(x)$ が含まれています。したがって、正常値ベースの外れ値検出とPU分類は互いに密接に関連しています。しかし、重要な違いは、正常値ベースの外れ値検出ではサンプルの外れ値を評価するための外れ値スコアが必要であるのに対し、PU分類では正と負のクラス間の閾値が必要であることです。この違いのため、式 (11) にはクラスの事前確率 $p(y = 1) = \pi$ も含まれています。

それでも、 f -divergence 推定の密度比フレームワークをPU分類に利用することができます。実際、

ここで、 $\overline{f}^*$ は損失関数に対応します。注目すべきは、式 (12) が